Обратная связь присуща всем процессам. Доказательство.

Саночкин В.В.

Аннотация.  ⇓ 

На основании определения обратной связи доказывается, что она действует во всех процессах без исключения. Классификация обратных связей дополнена нейтральными обратными связями, которые действуют в любом процессе, поддерживая безразличное равновесие и аддитивность контролируемых ими параметров, а также инерционность процесса. Приведены примеры нейтральных обратных связей, в частности, показано, что без них невозможно движение. Показано, что обратные связи действуют в системах любых масштабов и любой сложности.

.

Это отредактированная, дополненная и адаптированная для сайта версия статьи – Саночкин В.В. «Обратная связь присуща всем процессам без исключения», опубликованной в журнале Сложные системы, 2018, №1 (26), с.53-59 и выложенной в pdf-формате на данном сайте здесь. 

Интернет-страницу номера журнала «Сложные системы» можно посмотреть здесь. 

Содержание.  ⇑ 

• 1. Введение. 
• 2. Доказательство наличия обратной связи в любом процессе.
• 3. Дополненная классификация обратных связей.
• 4. Примеры нейтральных обратных связей.
• 5. Некоторые обобщения.
• 6. Независимость выводов от масштаба рассмотрения.
• 7. Заключение.
•     Литература.   

1. Введение.  ⇑ 

В наиболее общем случае обратной связью (ОС) называют влияние текущего результата процесса на дальнейшее его протекание [3,6]. Обычно, это влияние изображают в виде петли ОС (рис.1). Если ОС действует внутри процесса, как, например, при взрыве, то это внутренняя ОС, если иначе, например, с выхода на вход электронного усилителя по внешнему звуковому каналу, то это внешняя ОС.

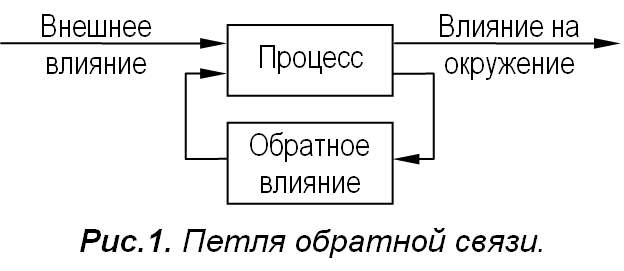ОС действуют в физических, биологических, социальных, психических и других видах процессов, в естественных и искусственных системах, широко используются в технике. Упоминания об этом можно найти в [1-5] и других многочисленных источниках. Во многих публикациях подчёркивается важность учета ОС. Например, в [2] отмечается: «Описывая явления, мы должны считать обратную связь основным процессом развития», или в [5 с.278]: «Сам принцип обратной связи для всего живого является настолько фундаментальным, что не учитывать его постоянное законное присутствие просто невозможно». Поэтому развитие представлений об ОС весьма важно и актуально.

По воздействию на процессы различают два вида ОС [3]: положительные, которые увеличивают интенсивность процесса, и отрицательные, которые её уменьшают. Обычно подразумевается, что бывают процессы без ОС. Например, в прямолинейном движении материальной точки ОС, обычно, не усматривается. Однако, несмотря на общепринятость, такие представления о классификации и распространённости ОС неполны.

Ниже на основании приведённого определения доказано, что ОС действуют во всех процессах без исключения, причём кроме перечисленных видов существуют ещё нейтральные ОС.  

2. Доказательство наличия обратной связи в любом процессе.  ⇑  

Для начала, рассмотрим взрыв в виде цепной реакции распада молекул взрывчатого вещества (например, тротила), где действие ОС является обще­признанным фактом [3]. Нам надо понять, как в этом, по сути, линейном во времени процессе усматривается петля ОС.

Чтобы инициировать взрыв, во взрывчатое вещество надо ввести энергию, достаточную для распада хотя бы одной молекулы этого вещества. Распавшаяся молекула выделяет энергию, достаточную для распада ещё нескольких таких же молекул. Пусть это будут 2 молекулы. Они развалят уже 2²=4 молекулы, те 2³=8 молекул, и на n-ом шаге распадётся 2ⁿ молекул, выделив энергию, достаточную для распада 2ⁿ⁺¹ молекул. Взрыв заканчивается, когда распались все молекулы взрывчатки, и высвободившаяся энергия разрушает уже не взрывчатку, а окружающие объекты. В реальности взрывчатка поглощает на каждом шаге не всю выделенную энергию, но мы пока отвлечемся от этого. Описанный процесс не зря называют цепной реакцией, он является линейной цепочкой шагов, изображенной на рис.2.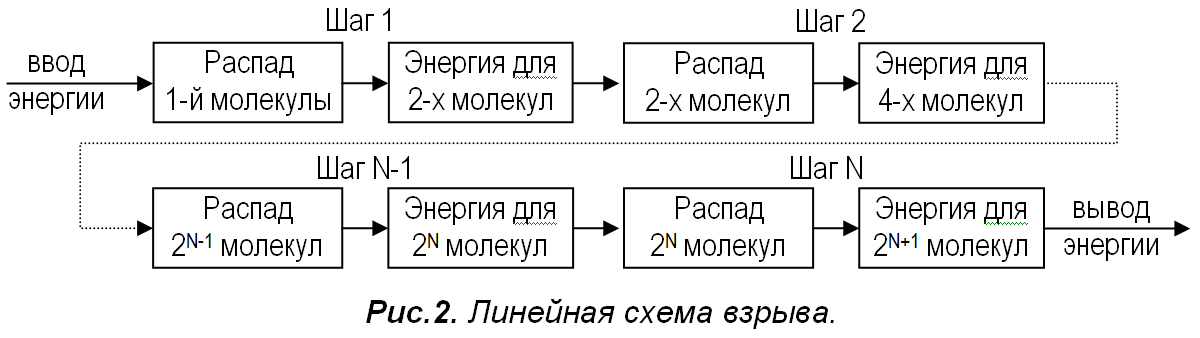

Получаемый на каждом шаге результат – выделенная энергия – влияет на продолжение процесса: чем больше энергии выделилось, тем интенсивнее пойдёт процесс дальше. Значит, по определению это процесс с ОС, причём положительной.

Бросается в глаза, что схема на рис.2 состоит из функционально повторяющихся звеньев. Это позволяет представить процесс более компактно в виде цикла, который изображен на рис.3. Здесь уже ясно видна петля ОС, как на рис.1. Причём из рис.2 следует, что связи в петле замыкаются внутри процесса, и данная ОС является внутренней.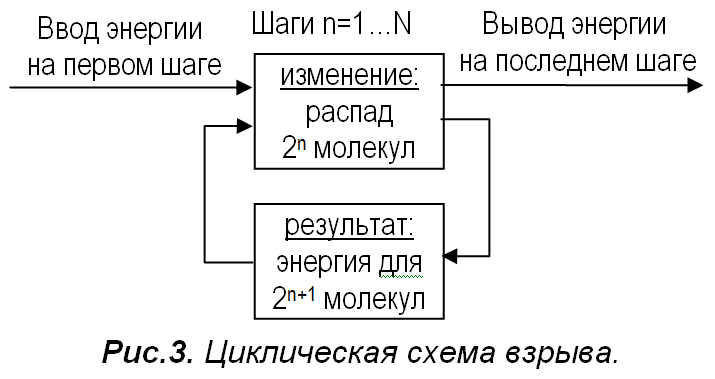

Теперь рассмотрим произвольный автономный процесс. Специфика автономного процесса состоит в том, что он запускается внешним воздействием, далее идёт автономно, то есть, без связи с внешним окружением, и лишь по окончанию выдаёт результат вовне. Разобьём процесс на шаги по времени (рис.4). На каждом шаге происходят изменения, результат которых полностью используется на следующем шаге, влияя на дальнейший ход процесса. Значит, в любом автономном процессе действует ОС.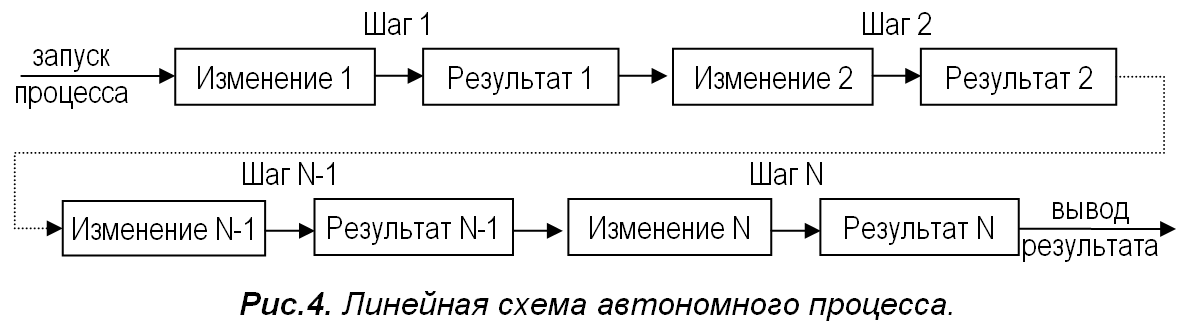

Линейная цепь шагов на рис.4 опять состоит из повторяющихся звеньев. Это позволяет свёрнуть её в петлю ОС (рис.5), связи в которой, как видно из рис.4, тоже являются внутренними относительно процесса.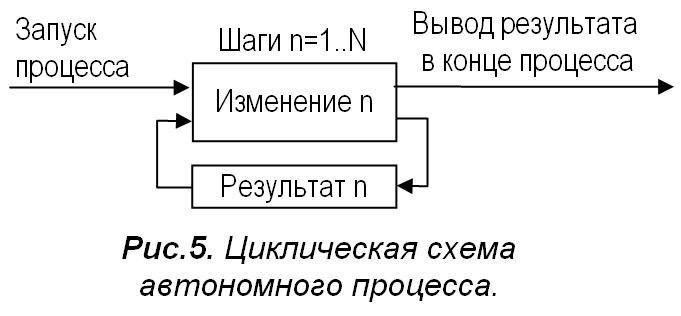  

Произвольный процесс отличается от автономного лишь структурой внешних связей. Внешнее влияние и частичный вывод результата возможны в нём на каждом шаге. Топология внутренних связей в обоих процессах одинакова. Это отображено на рис.6, из которого видно, что в произвольном процессе тоже действует внутренняя ОС. На практике это подтверждается тем, что текущий результат любого процесса влияет на дальнейшее его протекание, то есть любой процесс соответствует определению ОС.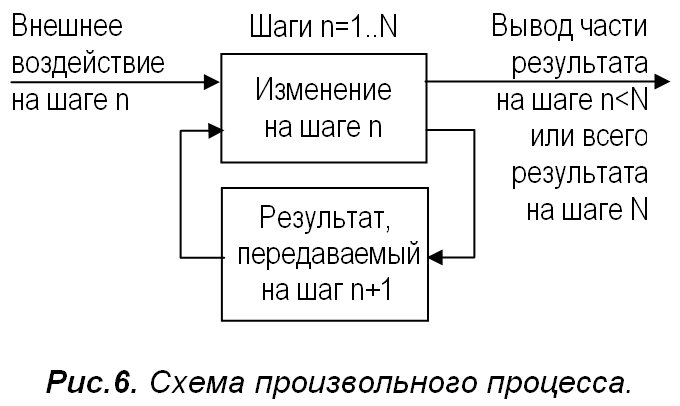

Может показаться, что процесс без ОС всё же возможен, если на каждом шаге выводить из него весь результат, ничего не оставляя для передачи по петле. Однако удаление из процесса всего текущего результата либо невозможно, либо завершает процесс. Действительно, любой процесс является эволюцией состояния системы участвующих в нём объектов, а состояние присуще системе неотъемлемо. Его невозможно вывести из процесса, и оно неминуемо передаётся от шага к шагу, пока существует система. Например, когда в процессе участвуют материальные объекты, на следующий шаг неизбежно передаются вещество, поля и достигнутые значения их пространственных и энергетических характеристик. То есть, пока процесс продолжается, состояние системы участвующих в нём объектов неминуемо передаётся от шага к шагу, влияя на его течение, и ОС действует. Как только ОС перестаёт действовать, петля на рис.6 разрывается, и на очередной шаг процесса не передаётся ничего, включая материю, энергию и информацию. Лишённый отправной точки и необходимых ресурсов этот шаг становится невозможным. В результате процесс завершается вместе с ОС. Например, без ОС останавливается взрыв и, как показано ниже, невозможно движение.

Иллюзия отсутствия ОС может возникать также в том случае, когда наблюдатель интересуется лишь входом и выходом процесса, а сам процесс не рассматривает. При этом процесс выступает для него «черным ящиком», в котором внутренние ОС скрыты. Как показано, внимательное рассмотрение процесса эту иллюзию опровергает.

Итак, наши рассуждения приводят к выводу, что внутренняя ОС является необходимым условием протекания любого процесса, и процессов без ОС не бывает, что мы и собирались доказать.  

3. Дополненная классификация обратных связей.  ⇑  

Присутствие ОС во всех процессах требует полноты её классификации. Эту классификацию удобно производить на основе петлевого коэффициента изменения контролируемого параметра: К_P = Р_n/Р_n‑1, где Р_n и Р_n‑1 – значения контролируемого параметра Р, соответственно, на шаге n и n‑1 в отсутствие внешних влияний.

• При К_P>1 параметр Р растёт, и OC называется положительной. Так, в примере со взрывом положительная ОС при К_P=2 действовала относительно числа распавшихся на шаге молекул и выделенной ими энергии.
• При К_P<1 контролируемый параметр стремится к нулю, и OC называют отрицательной. Примером может служить отклонение ракеты от цели при наведении.
• Когда К_P=1, контролируемый параметр сохраняется неизменным, и ОС резонно называть нейтральной.

Существование нейтральных ОС логично заполняет разрыв между положительными и отрицательными ОС, обеспечивая требуемую полноту классификации. При этом отрицательные ОС поддерживают устойчивость, положительные – неустойчивость, а нейтральные – безразличное равновесие контролируемых ими параметров. Именно такое назначение нейтральных ОС иллюстрируют примеры.  

4. Примеры нейтральных обратных связей.  ⇑  

Для примера возьмём движение материальной точки, упомянутое в начале статьи, как случай предполагаемого отсутствия ОС. Покажем, что в нём действует внутренняя ОС по состоянию точки. Для этого рассмотрим перемещение точки с массой m по оси X под действием постоянной силы F. Разобьём движение на равные шаги ∆t по времени t так, чтобы шаг n начинался при t=(n‑1)·∆t и заканчивался при t=n·∆t. На каждом шаге меняются импульс точки p на ∆p=F∆t и её положение x на ∆x=(p_n‑1+∆p/2)·∆t/m. Результаты n‑го шага – новые значения импульса р_n=p_n‑1+∆p и положения x_n=x_n‑1+∆x. Индексы n‑1 помечают результаты предыдущего шага, а при n=1 – начальные значения. Изобразим всё это в виде цикла на рис.7.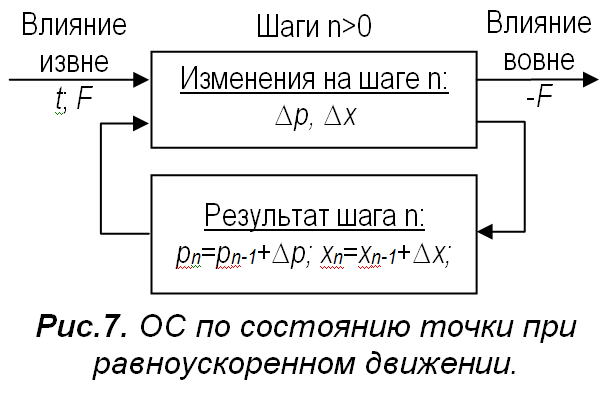 Вот какова петля ОС по состоянию точки при равноускоренном движении. Её можно разделить на две петли: по p и по x, тем самым, выделив процессы изменения каждого из параметров состояния. Эти петли образуют причинно-следственную иерархию, так как ∆x в петле по x в соответствии с приведённым выше выражением определяется средним значением p на том же шаге. Поэтому с алгоритмической точки зрения шаг в нашей дискретной модели должен быть разделён на два последовательных этапа. Сначала реализуется шаг в петле по p, в котором определяется среднее значение p, а после – шаг в петле по x, зависящей от p. При уменьшении ∆t, то есть при переходе от дискретного описания движения к непрерывному, среднее может быть сколь угодно близко к мгновенному, и разделение шага на этапы становится неактуальным.

Импульс р на шаге n складывается из двух частей: изменения импульса внешней силой ∆p=F∆t, и импульса p_n‑1, достигнутого на шаге n‑1 и переданного по петле ОС. Внутренние процессы в петле ОС не меняют р, что легко проверяется обнулением F. Поэтому К_р=1, и ОС по импульсу является нейтральной. Она обеспечивает действие закона сохранения импульса. Разрыв петли на рис.7 приводит к нарушению этого закона, так как импульс уже не может сохраняться во времени и быть итогом внешних воздействий. Даже само движение как накопление пошаговых изменений становится невозможным.

Положение точки подобно импульсу складывается также из двух частей: пошагового изменения ∆x и значения x, достигнутого на предыдущем шаге. Первое обусловлено импульсом p, который является внешней причиной по отношению к петле по x, а второе передаётся в этой петле неизменным, что проверяется обнулением p. Следовательно, К_x=1, и ОС по x аналогично ОС по p является нейтральной.

В отсутствие внешней силы движение становится равномерным и поддерживается только внутренней нейтральной ОС по импульсу, которая, реализуя закон сохранения, обеспечивает безразличное равновесие любого заданного значения p. Когда p=0, точка становится неподвижной. При этом в чистом виде проявляется нейтральность ОС по x, обеспечивая безразличное равновесие положения точки. Такое равновесие является характерным проявлением нейтральных ОС.  

5. Некоторые обобщения.  ⇑  

Выделяя процессы изменения каждого из параметров состояния, как в предыдущем разделе, можно показать, что нейтральные ОС действуют в любой системе и обеспечивают безразличное равновесие её параметров, когда нет причин для их изменения. Нейтральные ОС, по сути, являются механизмом имманентной системной «памяти», которая обсуждается в [1, с.17]. Они позволяют любой системе хранить в себе текущий итог своей эволюции, обеспечивая аддитивность параметров во времени и эволюцию от достигнутого состояния. Благодаря этим ОС, система либо аддитивно накапливает в текущем состоянии свои изменения под действием внешних и внутренних причин, либо сохраняет это состояние, когда причин для изменений нет. Последнее можно назвать инерцией состояния.

Когда связи между параметрами образуют замкнутую цепь, возникают дополнительные ОС по каждой группе таких параметров. Например, если материальную точку в нашем примере упруго связать с началом отсчёта, то сила F станет зависеть от положения точки: F=-kx, где k – постоянный коэффициент. В результате, цепочка связей замкнётся, и возникнет ОС, которая при ненулевых начальных условиях приведёт к бесконечным колебаниям всех трёх связанных в кольцо параметров: F, p, x.

Наконец, наши рассуждения приводят к выводу, что благодаря нейтральным обратным связям любые процессы обладают инерцией, то есть не изменяют свои параметры без причин. Причём для изменения существуют только два вида причин: внешние воздействия на параметры процесса и внутренние влияния одних его параметров на другие. Так, в примере с движением материальной точки её импульс p изменяется из-за влияния внешней силы F, а положение x – из-за внутренней зависимости от p. Тогда любой процесс можно представить, как систему характеризующих его параметров, охваченную обратной связью и управляемую внешними и внутренними воздействиями, что позволяет рассматривать его с позиций кибернетики.  

6. Независимость выводов от масштаба рассмотрения.  ⇑  

Приведённое доказательство всеобщего характера ОС никак не ограничивает виды процессов, к которым это относится. Дополнительно независимость сделанных выводов от рамок рассмотрения ситуации наблюдателем подкрепляют следующие соображения.

Если наблюдается только конкретная система, то с её уничтожением прекращаются процесс эволюции её состояния, внутренняя ОС по этому состоянию и сам процесс наблюдения этой системы. Например, исчерпание взрывчатки прекращает и ОС по её состоянию, и химическую реакцию. То есть процесс и внутренняя ОС в нём действуют и прекращаются одновременно.

Если в рассмотрение включена надсистема, то процесс эволюции её состояния продолжается, несмотря на разрушение некоторой её подсистемы, а ОС лишь меняет свой характер. Это можно проследить на том же примере взрыва, если рассматривать не только взрывчатку, но также продукты её распада и её окружение. В этом случае процесс не заканчивается с исчерпанием взрывчатки, а продолжается в виде релаксации продуктов взрыва в окружающей среде. При этом действует внутренняя ОС по состоянию этих продуктов и среды, в которую они проникают.

Если в предельном случае в качестве системы рассматривается вся природа во всём её многообразии, то процесс эволюции её состояния не заканчивается никогда, и ОС по этому состоянию действует постоянно. Причём одновременно могут действовать многочисленные ОС разных типов и по разным параметрам, охватывая как систему в целом, так и отдельные её части [1,3]. Так, при взрыве против рассмотренной ОС по выделенной энергии, замедляя процесс, работает неучтённая нами ОС по оставшейся взрывчатке: чем меньше её осталось, тем меньшая доля выделенной энергии в ней поглощается. Выше показано, что множественность внутренних ОС наблюдается даже при движении материальной точки.

Как видим, вывод о присутствии ОС в любых процессах не зависит от масштаба рассмотрения и сложности систем.  

7. Заключение.  ⇑  

На основании определения обратной связи доказано, что внутренняя обратная связь является условием протекания любого процесса, или другими словами, процессов без обратной связи не бывает. Это означает, что обратная связь должна быть отнесена к разряду фундаментальных характеристик природы, наряду с взаимодействием, в котором она всегда присутствует.

Общепринятая классификация, выделяет только положительные и отрицательные обратные связи, которые можно создавать и разрывать. Однако доказано, что для полноты эту классификацию необходимо дополнить нейтральными обратными связями, которые имманентно действуют во всех процессах и поддерживают аддитивность и безразличное равновесие контролируемых ими параметров. Благодаря нейтральным обратным связям все процессы обладают рядом универсальных свойств, а именно: самосогласованы, воспроизводят свою структуру и обладают инерцией, то есть не изменяются без причин. Например, нейтральная обратная связь по импульсу обеспечивает действие закона его сохранения и инерцию материальных тел при движении. Всем известная инерция мышления или отмеченная, например, в [4] инерционность социальных процессов, также объясняется нейтральными обратными связями.

Итак, любой процесс: изменение и неизменность любой системы; движение песчинки и планеты; развитие природы, человечества, организма и личности; научные исследования и художественное творчество; болезни, революции, катастрофы и войны – всё это процессы с внутренними обратными связями, и в них должны проявляться общие свойства и закономерности присущие таким процессам. По сумме приведённых соображений, изучение и учёт обратных связей должны являться важнейшими компонентами человеческой деятельности, и, как отмечено в [5 c.278], «понимание явлений и процессов во всем их логическом многообразии требует от человека целой "обратносвязевой" культуры мышления».   

Литература.  ⇑  

1. Гринченко С.Н. Метаэволюция (систем неживой, живой и социально-технической природы). – М.: ИПИРАН, 2007. – 456 с. 

2. Дюкрок А. Физика кибернетики. // Кибернетика – неограниченные возможности и возможные ограничения. Итоги развития. – М.: Наука, 1979, с.86-101. 

3. Жаботинский М.Е., Сенаторов К.Я. Обратная связь. – Физический энциклопедический словарь. М.: Советская энциклопедия, 1984, с.477-479. 

4. Малков С.Ю. Методологические аспекты логико-математического моделирования социально-исторических процессов. // Эволюция, 2003, №1, с.42-45. 

5. Палагин С.В. Полилогические раскопки. Саратов: ИКД Пароход, 2000. – 485 с. 

6. Фрейдин Л.И. Обратная связь. – БСЭ, т.18. М.: Советская энциклопедия, 1974, с.222.

.

 _⇑_